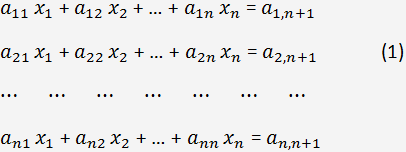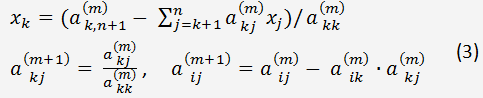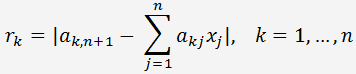Řešení soustav lineárních rovnic

Řešení soustavy lineárních algebraických rovnic

Možnosti univerzální kalkulačky: řešení soustavy lineárních rovnic se dvěma neznámými, řešení soustavy algebraických rovnic se třemi neznámými, čtyř lineárních rovnic se čtyřmi neznámými, pět lineárních rovnic s pěti neznámými, atd. Největší počet rovnic v soustavě je 11.
Pro řešení soustavy rovnic, je nutné zadat počet rovnic a odpovídající koeficienty.

Řešení soustav lineárních rovnic pomocí Gaussovy eliminační metody

Řešení soustav rovnic pomocí determinantů je vhodné provádět u soustav s 2 a 3 rovnicemi. Pro větší počet rovnic je mnohem výhodnější použít Gaussovou eliminaci. Gaussova eliminace je založena na postupném odčítání neznámých. Gaussovou eliminační metodou lze rychle řešit soustavu n rovnic o n neznámých.

Gaussova eliminační metoda pro řešení soustav algebraických rovnic:

Krok 1. Dopředné redukci : úpravíme matice soustavy na schodový tvar.

Krok 2. Zpětné substituci: nalezení řešení soustavy pomocí zpětné substituce.

Najděme řešení následující soustavy rovnic pomocí Gaussovy eliminace:



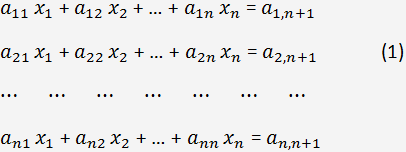
kde x_i jsou neznámé, i = 1, 2,..., n; n < 200. Pokud je počet rovnic větší, je nutné použít iterační metody řešení.
a_i,j - prvky rozšířené matice koeficientů.

V souladu s Gaussovou eliminační metodou najdeme x ₁ z první rovnice
x₁ = (a_1,n+1 - a_1,2x₂ - ... - a_1nx_n)/a₁₁     (2)
Pokud a_1,1 = 0, je nutné změnit uspořádání rovnic soustavy.

Pak nahradíme (2) do všech rovnic soustavy (1), s výjimkou první rovnice. Tak bude neznámý x ₁ odstraněn ze všech rovnic soustavy, s výjimkou první rovnice.

Prvky rozšířené matice budou transformované podle vzorce:
a_1j⁽¹⁾ = a_1j/a₁₁

a_ij⁽¹⁾ = a_ij - a_i1a_1j⁽¹⁾, i = 2,3,...,n; j = 1, 2,..., n+1.

V důsledku výjimky x ₁ ze všech rovnic, vše prvky prvního sloupce transformované matice budou nulové, s výjimkou a₁₁⁽¹⁾ = 1.

Podobně vyjádřím x₂ z 2. rovnice a odstraním ze zbývajících rovnic soustavy, atd.

Získáme transformovanou matici, ve které všechny prvky pod hlavní diagonálou jsou nulové.

Zapíšeme vzorec pro vyloučení neznámého x_k a získání koeficientů transformované matice.


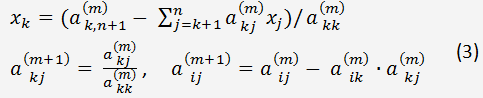
Nyní můžeme určit všechny neznámé x_k postupně od x_n do x₁. Tento postup se nazývá zpětný chod.
Za účelem snížení chyby při dělení na diagonální prvek ve vzorce (3), se doporučuje změnit uspořádání rovnic soustavy tak, abychom měli na úhlopříčce největší v absolutní hodnotě ze všech prvků příslušného sloupce. Tato modifikace Gaussovy eliminační metody, která slouží ke zmenšení zaokrouhlovacích chyb, se nazývá eliminace s výběrem hlavního prvku.

Odhadnout chybu numerického řešení soustavy je možné pomocí výpočtu diskrepance. K tomu je nutné nahradit numerické řešení x_k, k = 1, 2,..., n do soustavy a vypočítat rozdíl mezi pravou a levou stranami rovnic.

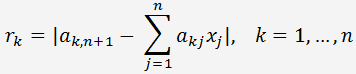
Při malé chybě řešení, velikost r_k bude nulová.