Řešení soustav tří lineárních rovnic se třemi neznámými
Kalkulačka provádí výpočet soustavy lineárních rovnic o třech neznámých 3x3. Pro řešení soustavy rovnic se třemi neznámými pomocí kalkulačky, zadejte koeficienty a klikněte "Vyřešit".
Cramerovo pravidlo pro řešení soustavy lineárních rovnic
Cramerovo pravidlo umožňuje řešit soustavy
n lineárních rovnic o
n neznámých, kde matice soustavy rovnic představuje regulární matici řádu n. Nejčastěji Cramerovo pravidlo využívají pro soustavy dvou a tří lineárních rovnic, protože výpočty determinantů čtvrtého a vyšších řádů jsou dost náročné. Cramerovo pravidlo je vhodné pro řešení čtverečních soustav lineárních algebraických rovnic, u kterých determinant hlavní matice je různý od nuly. Pokud není Cramerovo pravidlo použitelné, můžeme vyřešit soustavu rovnic pomocí Gaussovy eliminační metody.
Je dána soustava n lineárních rovnic o n neznámých x
1, x
2, ..., x
n:
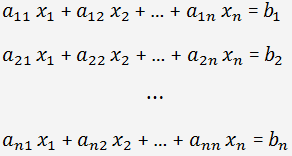
Protože matice teto soustavy rovnic má n řádků a n sloupců, je čtvercová.
Označme determinant:
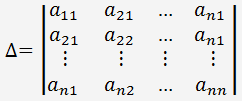
Označme
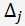
determinant matici, která vznikla nahrazením j−tého sloupce sloupcem pravých stran soustavy rovnic
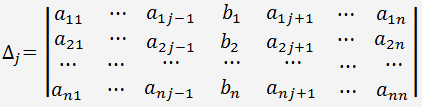
Je-li determinant nenulový
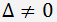
, soustava má jedno řešení.
Řešení soustavy lineárních rovnic najdeme přes Cramerovo pravidlo:
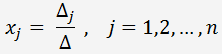
Přiklad. Najděme řešení následující soustavy tří lineárních rovnic se třemi neznámými pomocí Cramerova pravidla.
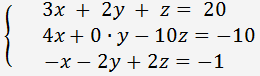
Determinant matice soustavy je nenulový, proto lze použít Cramerovo pravidlo.
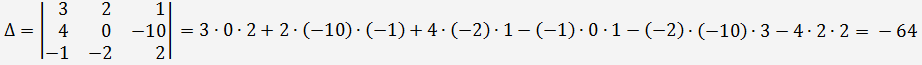
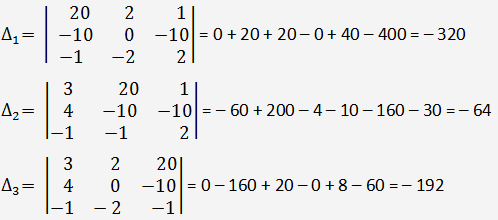
Podle Cramerova pravidla
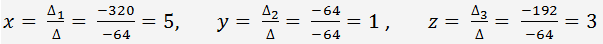
Řešení soustavy lineárních rovnic (Gaussova eliminační metoda)
Přiklad. Řešení soustavy tří lineárních rovnic o třech neznámých pomocí Gaussovy eliminační metody.
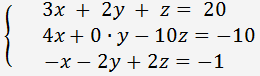
Vydělíme první rovnice soustavy 3
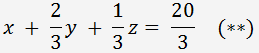
Násobíme rovnice (**) 4 a odečteme od druhé rovnici, pak násobíme rovnice (**) -1 a odečteme od třetí rovnice. Získáme následující soustavu rovnic
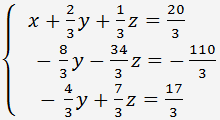
Vydělíme druhou rovnici
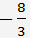
a získáme
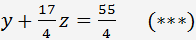
Násobíme rovnice (***)
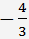
a odečteme od třetí rovnice. Máme soustavu rovnic
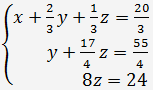
Z poslední rovnice nacházíme z = 3. Dosadíme výsledek do druhé rovnice:
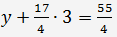
=> y = 1.
Dosadíme
y a
z do první rovnici a zjistíme
x 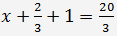
=> x = 5.
Výsledek: x = 5, y = 1, z = 3.

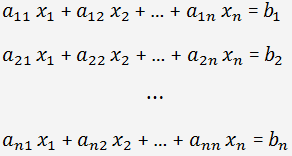
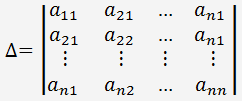
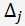 determinant matici, která vznikla nahrazením j−tého sloupce sloupcem pravých stran soustavy rovnic
determinant matici, která vznikla nahrazením j−tého sloupce sloupcem pravých stran soustavy rovnic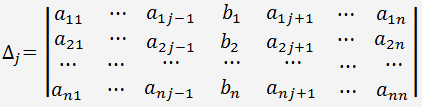
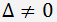 , soustava má jedno řešení.
, soustava má jedno řešení.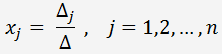
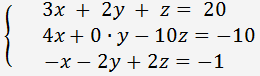
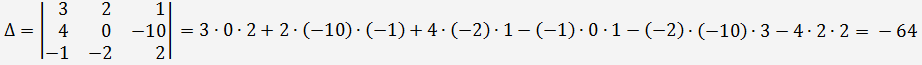
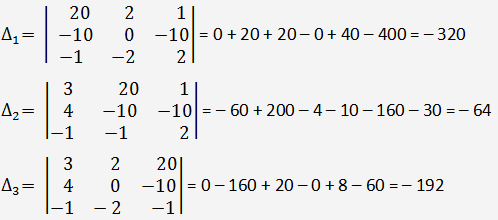
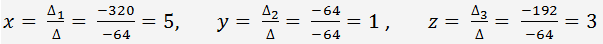
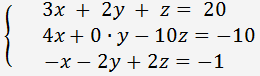
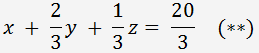
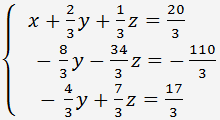
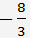 a získáme
a získáme 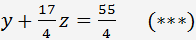
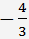 a odečteme od třetí rovnice. Máme soustavu rovnic
a odečteme od třetí rovnice. Máme soustavu rovnic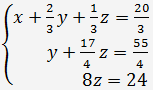
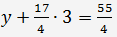 => y = 1.
=> y = 1.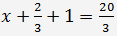 => x = 5.
=> x = 5.