Řešení soustavy dvou lineárních rovnic o dvou neznámých
Soustava dvou lineárních rovnic se dvěma neznámými může mít jedno řešení, nemít žádné řešení nebo mít nekonečně mnoho řešení.
Pro řešení soustav dvou lineárních rovnic o dvou neznámých existují tři metody: dosazovací metoda, sčítací metoda a grafická metoda.
Kalkulačka pro výpočet soustavy dvou rovnic o dvou neznámých 2x2
Kalkulačka je jednoduchý nástroj pro výpočet soustavy rovnic o dvou neznámých.
Chcete-li vyřešit soustavu dvou rovnic se dvěma neznámými 2x2 pomocí kalkulačky, stačí zadat koeficienty soustavy rovnic a kliknut tlačítko "Vyřešit".
Řešení soustavy dvou lineárních rovnic se dvěma neznámými dosazovací metodou.
Při řešení soustavy dvou lineárních rovnic se dvěma neznámými dosazovací metodou, z jedné rovnice, buď první nebo druhé, vyjádříme jednu neznámou pomocí druhé neznámé a získaný výraz dosadíme do jiné rovnice, čímž vyloučíme jednu neznámou z této rovnice. Dostaneme tak lineární rovnici s jednou neznámou, kterou mužeme vyřešit. Pak
vypočítanou hodnotu dosadíme do první rovnice a vypočítáme druhou neznámou.
Přiklad 1. Řešení soustavy lineárních rovnic o dvou neznámých dosazovací metodou.
Máme soustavu rovnic:
3x - 2y = 10
5x + y = 21
Z první rovnice vyjádříme neznámou
y:
y = (3x - 10)/2
Získaný výraz dosadíme do druhé rovnice a dostaneme rovnici s jednou neznámou:
5x + (3x - 10) / 2 = 21
Z této rovnici vypočítáme
x:
3x - 10 = 2(21 - 5x)
3x - 10 = 42 - 10x
13x = 52
x = 4
Vypočítanou hodnotu
x dosadíme do první rovnice:
3*4 - 2y = 10
2y = 12 - 10
y = 1
Řešení soustavy: x = 4, y = 1.
Řešení soustavy dvou lineárních rovnic se dvěma neznámými sčítací metodou.
Při řešení soustavy dvou lineárních rovnic o dvou neznámých sčítací metodou, rovnice vynásobíme takovými čísly, aby se po sečtení rovnic jedna neznámá vyloučila a jsme dostali jednu lineární rovnici s jednou neznámou.
Přiklad 2. Najděme řešení následující soustavy dvou lineárních rovnic se dvěma neznámými sčítací metodou.
3x - 2y = 10
5x + y = 21
Vynásobíme druhou rovnici 2, aby koeficienty u neznámé
y v první i ve druhé rovnici byla opačná čísla.
3x - 2y = 10
5x + y = 21 *(2)
3x - 2y = 10
10x + 2y = 42
Rovnice sečteme a vypočítáme neznámou
x:
13x = 52
x = 4
Vypočítanou hodnotu
x dosadíme do libovolné rovnice a vypočteme
y:
3*4 - 2y = 10
2y = 2
y = 1
Řešení soustavy rovnic: x = 4, y = 1.
Řešení soustavy dvou lineárních rovnic o dvou neznámých (Cramerovo pravidlo)
Cramerovo pravidlo se používá pro řešení soustavy lineárních rovnic s regulární maticí. Regulární matice je čtvercová matice, u které determinant je různý od nuly.
Cramerovo pravidlo je vhodné pro soustavy dvou a tří rovnic, protože výpočet determinantů čtvrtého a vyšších řádů je náročný postup.
Uvažujeme soustavu n lineárních rovnic o n neznámých x
1, x
2, ..., x
n:
a
11x
1 + a
12x
2 + ...+ a
1nx
n = b
1
a
21x
1 + a
22x
2 + ...+ a
2nx
n = b
2
... ... ... ... ...
a
n1x
1 + a
n2x
2 + ...+ a
nnx
n = b
n
Matice koeficientů je čtvercová matice, protože má n řádků a n sloupců. Označme determinant matice soustavy lineárních rovnic:
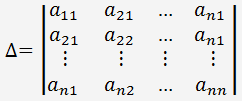
Označme
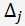
jako determinant matice soustavy lineárních rovnic, ve které je j-tý sloupec nahrazen sloupcem pravých stran soustavy rovnic.
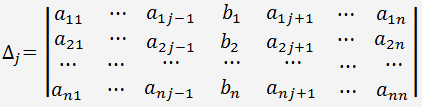
Pokud je determinant matice soustavy nenulový
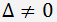
, matice je regulární a soustava má jedno řešení
pro které platí:
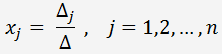 Přiklad 3.
Přiklad 3. Vyřešíme následující soustavu pomocí Cramerova pravidla.
Nechť máme soustavu dvou lineárních rovnic se dvěma neznámými
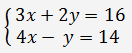
Poněvadž determinant matice soustavy je nenulový, lze použít Cramerovo pravidlo.
Podle Cramerova pravidla
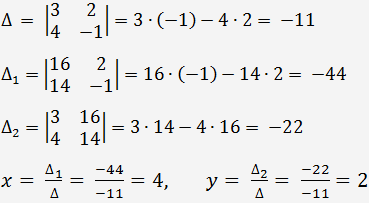
Řešení soustavy rovnic: x = 4, y = 2.
Gaussova eliminační metoda pro řešení soustavy lineárních rovnic
Princip řešení soustavy lineárních rovnic pomocí Gaussovy eliminační metody je založen na postupné převedení soustavy rovnic pomocí elementárních řádkových úprav do soustavy řádkově odstupňovaného tvaru, která je ekvivalentní s původní soustavou a pak nalezení řešení soustavy pomocí zpětné substituce.
Příklad 4. Řešení soustavy dvou lineárních rovnic se dvěma neznámými pomocí Gaussovy eliminace.
Soustava dvou lineárních rovnic o dvou neznámých:
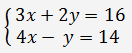
Vydělíme první rovnice soustavy 3
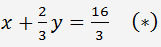
Násobíme (*) 4 a odečteme od druhé rovnici. Získáme následující soustavu rovnic
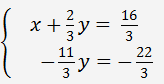
Získáme řešení y = 2. V prvním řádku dosadíme za
y a vyřešíme
x:
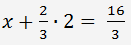
.
Řešení soustavy rovnic: x = 4, y = 2.
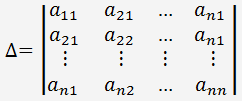
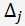 jako determinant matice soustavy lineárních rovnic, ve které je j-tý sloupec nahrazen sloupcem pravých stran soustavy rovnic.
jako determinant matice soustavy lineárních rovnic, ve které je j-tý sloupec nahrazen sloupcem pravých stran soustavy rovnic.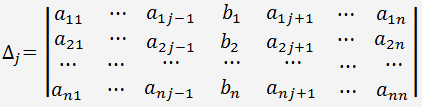
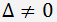 , matice je regulární a soustava má jedno řešení
, matice je regulární a soustava má jedno řešení 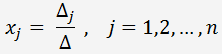
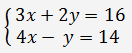
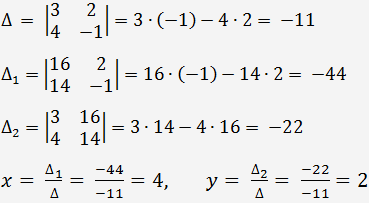
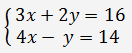
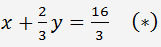
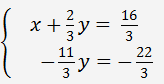
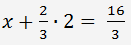 .
.